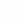TED日本語 - ケイティ・バウマン: ブラックホールの写真を撮影する

In the movie "Interstellar," we get an up-close look at a supermassive black hole. Set against a backdrop of bright gas, the black hole's massive gravitational pull bends light into a ring. However, this isn't a real photograph, but a computer graphic rendering -- an artistic interpretation of what a black hole might look like.

A hundred years ago, Albert Einstein first published his theory of general relativity. In the years since then, scientists have provided a lot of evidence in support of it. But one thing predicted from this theory, black holes, still have not been directly observed. Although we have some idea as to what a black hole might look like, we've never actually taken a picture of one before. However, you might be surprised to know that that may soon change. We may be seeing our first picture of a black hole in the next couple years. Getting this first picture will come down to an international team of scientists, an Earth-sized telescope and an algorithm that puts together the final picture. Although I won't be able to show you a real picture of a black hole today, I'd like to give you a brief glimpse into the effort involved in getting that first picture.

My name is Katie Bouman, and I'm a PhD student at MIT. I do research in a computer science lab that works on making computers see through images and video. But although I'm not an astronomer, today I'd like to show you how I've been able to contribute to this exciting project.

If you go out past the bright city lights tonight, you may just be lucky enough to see a stunning view of the Milky Way Galaxy. And if you could zoom past millions of stars,26,000 light-years toward the heart of the spiraling Milky Way, we'd eventually reach a cluster of stars right at the center. Peering past all the galactic dust with infrared telescopes, astronomers have watched these stars for over 16 years. But it's what they don't see that is the most spectacular. These stars seem to orbit an invisible object. By tracking the paths of these stars, astronomers have concluded that the only thing small and heavy enough to cause this motion is a supermassive black hole -- an object so dense that it sucks up anything that ventures too close -- even light.

But what happens if we were to zoom in even further? Is it possible to see something that, by definition, is impossible to see? Well, it turns out that if we were to zoom in at radio wavelengths, we'd expect to see a ring of light caused by the gravitational lensing of hot plasma zipping around the black hole. In other words, the black hole casts a shadow on this backdrop of bright material, carving out a sphere of darkness. This bright ring reveals the black hole's event horizon, where the gravitational pull becomes so great that not even light can escape. Einstein's equations predict the size and shape of this ring, so taking a picture of it wouldn't only be really cool, it would also help to verify that these equations hold in the extreme conditions around the black hole.

However, this black hole is so far away from us, that from Earth, this ring appears incredibly small -- the same size to us as an orange on the surface of the moon. That makes taking a picture of it extremely difficult. Why is that? Well, it all comes down to a simple equation. Due to a phenomenon called diffraction, there are fundamental limits to the smallest objects that we can possibly see. This governing equation says that in order to see smaller and smaller, we need to make our telescope bigger and bigger. But even with the most powerful optical telescopes here on Earth, we can't even get close to the resolution necessary to image on the surface of the moon. In fact, here I show one of the highest resolution images ever taken of the moon from Earth. It contains roughly 13,000 pixels, and yet each pixel would contain over 1.5 million oranges.

So how big of a telescope do we need in order to see an orange on the surface of the moon and, by extension, our black hole? Well, it turns out that by crunching the numbers, you can easily calculate that we would need a telescope the size of the entire Earth.

(Laughter)

If we could build this Earth-sized telescope, we could just start to make out that distinctive ring of light indicative of the black hole's event horizon. Although this picture wouldn't contain all the detail we see in computer graphic renderings, it would allow us to safely get our first glimpse of the immediate environment around a black hole.

However, as you can imagine, building a single-dish telescope the size of the Earth is impossible. But in the famous words of Mick Jagger, "You can't always get what you want, but if you try sometimes, you just might find you get what you need." And by connecting telescopes from around the world, an international collaboration called the Event Horizon Telescope is creating a computational telescope the size of the Earth, capable of resolving structure on the scale of a black hole's event horizon. This network of telescopes is scheduled to take its very first picture of a black hole next year. Each telescope in the worldwide network works together. Linked through the precise timing of atomic clocks, teams of researchers at each of the sites freeze light by collecting thousands of terabytes of data. This data is then processed in a lab right here in Massachusetts.

So how does this even work? Remember if we want to see the black hole in the center of our galaxy, we need to build this impossibly large Earth-sized telescope? For just a second, let's pretend we could build a telescope the size of the Earth. This would be a little bit like turning the Earth into a giant spinning disco ball. Each individual mirror would collect light that we could then combine together to make a picture. However, now let's say we remove most of those mirrors so only a few remained. We could still try to combine this information together, but now there are a lot of holes. These remaining mirrors represent the locations where we have telescopes. This is an incredibly small number of measurements to make a picture from. But although we only collect light at a few telescope locations, as the Earth rotates, we get to see other new measurements. In other words, as the disco ball spins, those mirrors change locations and we get to observe different parts of the image. The imaging algorithms we develop fill in the missing gaps of the disco ball in order to reconstruct the underlying black hole image. If we had telescopes located everywhere on the globe -- in other words, the entire disco ball -- this would be trivial. However, we only see a few samples, and for that reason, there are an infinite number of possible images that are perfectly consistent with our telescope measurements. However, not all images are created equal. Some of those images look more like what we think of as images than others. And so, my role in helping to take the first image of a black hole is to design algorithms that find the most reasonable image that also fits the telescope measurements.

Just as a forensic sketch artist uses limited descriptions to piece together a picture using their knowledge of face structure, the imaging algorithms I develop use our limited telescope data to guide us to a picture that also looks like stuff in our universe. Using these algorithms, we're able to piece together pictures from this sparse, noisy data. So here I show a sample reconstruction done using simulated data, when we pretend to point our telescopes to the black hole in the center of our galaxy. Although this is just a simulation, reconstruction such as this give us hope that we'll soon be able to reliably take the first image of a black hole and from it, determine the size of its ring. Although I'd love to go on about all the details of this algorithm, luckily for you, I don't have the time.

But I'd still like to give you a brief idea of how we define what our universe looks like, and how we use this to reconstruct and verify our results. Since there are an infinite number of possible images that perfectly explain our telescope measurements, we have to choose between them in some way. We do this by ranking the images based upon how likely they are to be the black hole image, and then choosing the one that's most likely.

So what do I mean by this exactly? Let's say we were trying to make a model that told us how likely an image were to appear on Facebook. We'd probably want the model to say it's pretty unlikely that someone would post this noise image on the left, and pretty likely that someone would post a selfie like this one on the right. The image in the middle is blurry, so even though it's more likely we'd see it on Facebook compared to the noise image, it's probably less likely we'd see it compared to the selfie.

But when it comes to images from the black hole, we're posed with a real conundrum: we've never seen a black hole before. In that case, what is a likely black hole image, and what should we assume about the structure of black holes? We could try to use images from simulations we've done, like the image of the black hole from "Interstellar," but if we did this, it could cause some serious problems. What would happen if Einstein's theories didn't hold? We'd still want to reconstruct an accurate picture of what was going on. If we bake Einstein's equations too much into our algorithms, we'll just end up seeing what we expect to see. In other words, we want to leave the option open for there being a giant elephant at the center of our galaxy.

(Laughter)

Different types of images have very distinct features. We can easily tell the difference between black hole simulation images and images we take every day here on Earth. We need a way to tell our algorithms what images look like without imposing one type of image's features too much. One way we can try to get around this is by imposing the features of different kinds of images and seeing how the type of image we assume affects our reconstructions. If all images' types produce a very similar-looking image, then we can start to become more confident that the image assumptions we're making are not biasing this picture that much.

This is a little bit like giving the same description to three different sketch artists from all around the world. If they all produce a very similar-looking face, then we can start to become confident that they're not imposing their own cultural biases on the drawings. One way we can try to impose different image features is by using pieces of existing images. So we take a large collection of images, and we break them down into their little image patches. We then can treat each image patch a little bit like pieces of a puzzle. And we use commonly seen puzzle pieces to piece together an image that also fits our telescope measurements.

Different types of images have very distinctive sets of puzzle pieces. So what happens when we take the same data but we use different sets of puzzle pieces to reconstruct the image? Let's first start with black hole image simulation puzzle pieces. OK, this looks reasonable. This looks like what we expect a black hole to look like. But did we just get it because we just fed it little pieces of black hole simulation images? Let's try another set of puzzle pieces from astronomical, non-black hole objects. OK, we get a similar-looking image. And then how about pieces from everyday images, like the images you take with your own personal camera? Great, we see the same image. When we get the same image from all different sets of puzzle pieces, then we can start to become more confident that the image assumptions we're making aren't biasing the final image we get too much.

Another thing we can do is take the same set of puzzle pieces, such as the ones derived from everyday images, and use them to reconstruct many different kinds of source images. So in our simulations, we pretend a black hole looks like astronomical non-black hole objects, as well as everyday images like the elephant in the center of our galaxy. When the results of our algorithms on the bottom look very similar to the simulation's truth image on top, then we can start to become more confident in our algorithms. And I really want to emphasize here that all of these pictures were created by piecing together little pieces of everyday photographs, like you'd take with your own personal camera. So an image of a black hole we've never seen before may eventually be created by piecing together pictures we see all the time of people, buildings, trees, cats and dogs. Imaging ideas like this will make it possible for us to take our very first pictures of a black hole, and hopefully, verify those famous theories on which scientists rely on a daily basis.

But of course, getting imaging ideas like this working would never have been possible without the amazing team of researchers that I have the privilege to work with. It still amazes me that although I began this project with no background in astrophysics, what we have achieved through this unique collaboration could result in the very first images of a black hole. But big projects like the Event Horizon Telescope are successful due to all the interdisciplinary expertise different people bring to the table. We're a melting pot of astronomers, physicists, mathematicians and engineers. This is what will make it soon possible to achieve something once thought impossible.

I'd like to encourage all of you to go out and help push the boundaries of science, even if it may at first seem as mysterious to you as a black hole.

Thank you.

(Applause)